Lentes de grande formato em câmeras pequenas

Muita gente tem a curiosidade de usar uma lente clássica de grande formato, como a Symmar, Sironar ou Planar, por exemplo, em uma câmera digital. Creio que a principal razão seja a vontade de usar essas ópticas lendárias e a dificuldade de se fazer fotografia em grande formato. A dificuldade começa pelo simples fato de ser fotografia analógica. Além do custo dos filmes há a necessidade de um laboratório bem equipado se o objetivo final for uma ampliação em papel de gelatina de prata.

Este artigo irá discutir o que se pode esperar dessa hibridização. Primeiro teoricamente e depois com um teste prático. O motivo pelo qual resolvi fazer essa verificação é porque gosto muito dessas ópticas antigas mas, pelo menos em teoria, o desempenho delas não deve ser melhor que de uma lente nativa do sistema digital. Caso seja melhor, é realmente ou por uma excelência totalmente fora da curva ou porque a óptica digital usada na comparação é realmente medíocre.

Ângulo de visão x formato do quadro

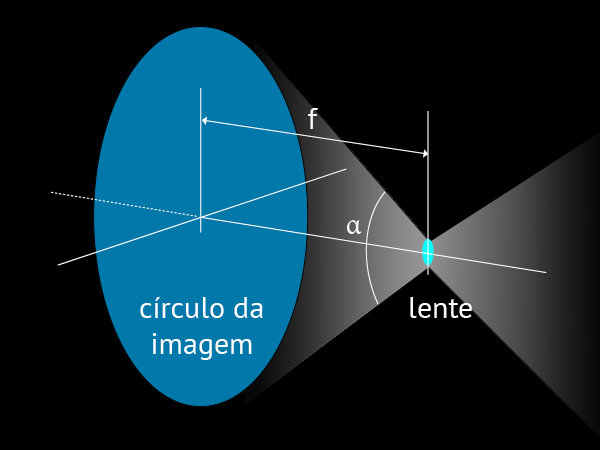A distância focal f e o ângulo de visão α determinam o círculo de imagem
e os possíveis formatos para a lente

 

O primeiro ponto a se observar é que estamos falando de lentes muito diferentes entre Grande Formato e outra desenhada para full-frame ou APSC.  Acostumamos a pensar em lentes do ponto de vista da distância focal, abertura e quadro. Mas o quadro é um dado relativo, é variável, não é inerente ao desenho da lente. As lentes são escaláveis. Se uma lente de 100 mm cobre um quadro de 1/4 de placa, o mesmo design escalado para 200 mm irá cobrir uma placa inteira. É por isso que nos tempos em que fotografia se fazia em muitos formatos diferentes as lentes eram oferecidas de 50 a 500 mm em às vezes algo como 15 opções de distância focal. Essa era a regra para os designs de sucesso como a Dagor da Goerz, por exemplo.

Já o ângulo de visão de um certo design, esse sim, é absoluto. Se uma lente é angular em uma focal curta ela continua sendo angular em uma focal longa. Salvo ajustes construtivos específicos para se conformar a um processo ou a uma câmera, quando pequenas variações podem ocorrer, lentes designadas com o mesmo nome, possuem essencialmente ângulos de visão iguais.

As três características realmente determinantes de uma lente são: distância focal, ângulo de visão e abertura máxima. Depois disso o que entra são aspectos de qualidade da imagem, do plano focal ser mais ou menos curvo, dela lidar bem ou mal com tal e tal aberração, mas esses três números são como que os especificadores chave de uma lente. O tamanho do quadro é só uma consequência da relação entre distância focal e ângulo de visão.

Ângulos grandes x ângulos estreitos

Enquanto que as lentes de ângulo grande são chamadas e entendidas como angulares ou super-angulares, o que corresponde mais ou menos a 70º e 110º, aproximadamente e respectivamente, não há um nome bom para as que cobrem apenas um ângulo estreito. “Foco longo” é usado mas creio que apenas alimenta a confusão, pois pelo que foi explicado acima, uma lente pode ter focal de 800 mm e ser uma grande angular. “Tele objetiva” é ainda pior pois na verdade refere-se a uma lente cujo centro óptico está localizado à frente de seu primeiro elemento, isto é, ela é mais curta fisicamente do que opticamente. Isso é comum nas câmeras 35mm para que uma lente de 300 mm não precise ter mais do que 300 de comprimento efetivo. Vou então adotar aqui o pouco usual mas correto ângulo estreito como contraposição a grande angular ou ângulo grande.

Em óptica a fabricação de lentes é muito mais simples quando estas possuem as superfícies esféricas. As a-esféricas só foram introduzidas comercialmente na segunda metade do século XX. A razão para isso é que mesmo uma calota de ferro redonda com uma precisão relativamente fraca em seu raio, de um ponto a outro de sua superfície, quando esfregada contra um bloco de vidro com abrasivos, consegue dar uma precisão ao raio de curvatura do vidro que ganha várias casas decimais em comparação com a calota original. Se quiser ver como se fabrica uma lente de modo bem artesanal, assista este vídeo sobre a restauração de uma lente histórica da Voigtlander. É esse princípio estatístico que faz o raio de curvatura do vidro ser uma média muito precisa de todos os imprecisos raios de curvatura do ferro. Isso permitiu que ótimas lentes tenham sido fabricadas desde o século XVIII quando houve um forte crescimento da indústria óptica para a astronomia.

O caso com as lentes esféricas é que elas geram um campo focal curvo e os filmes e sensores são fáceis de construir planos. Com esse conflito, a qualidade da imagem tende a ser boa apenas muito perto do eixo da lente, no ponto central da imagem e seu entorno mais próximo. Para quem lembra de matemática, é na região da base do cone onde o seno do ângulo do cone está muito parecido com o valor do próprio ângulo em radianos.

A consequência desse conflito de interesses entre a fabricação da lentes e a fabricação dos sensores/filmes é que é muito mais fácil se fabricar lentes com ângulos de visão estreitos do que lentes com ângulos de visão grandes. Isto é, exige-se muito mais elementos, muito mais cálculos e muito mais inspiração para se desenhar uma lente que consiga cobrir 45º ou 90º  do que uma que cubra apenas 8º ou 15º, com uma imagem nítida e pouco deformada.

A negociação

Para vencer a dificuldade em se desenhar lentes angulares há sempre uma negociação a ser feita pelo designer. Para aumentar o ângulo ele terá que sacrificar alguma coisa. A mais óbvia é a abertura. Uma lente excelente como a Protar V da Zeiss, com ângulo de 110º, tem sua abertura máxima em f/18, por exemplo. Outra possibilidade é abrir mão da qualidade da imagem na periferia da mesma. Isto significa admitir mais de aberrações e distorções. Mas enquanto que para uma lente de retratos pode-se mais facilmente admitir essa deterioração, nas grande angulares, mais voltadas para paisagens e arquitetura, deseja-se que sejam nítidas e sem distorções em todo o campo. Outra possibilidade é se admitir uma perda de resolução geral. Resolução é a capacidade que a lente tem de não confundir dois pontos muito próximos. Resolução ideal seria quando dois pontos no objeto correspondessem sempre a dois pontos na imagem. Mas isso nunca acontece. Nem mesmo nos nosso olhos. Um carro com dois faróis acesos mas ainda muito distante, aparece para nós como se tivesse apenas um farol. Nossa retina também tem uma resolução finita e apenas quando o nosso ângulo de visão separando os faróis for maior que ~0,02º é que veremos os dois distintamente. Tanto o sistema óptico como o sistema sensível (retina, filme ou sensor) possuem esse poder limitado de distinguir elementos contíguos em uma cena qualquer. Nos sistemas ópticos isso leva ao conceito de “círculo de confusão”. Ele é moeda na negociação do designer quando ele vai projetar uma lente. Para ganhar mais ângulo, normalmente, abre mão do poder de resolução da lente.

Círculo de confusão x formato

Os pontos no objeto e os pontos na imagem fotográfica, no mundo real, são na verdade como que superfícies e não pontos. Com cálculo infinitesimal pode-se aproximar estas superfícies para pontos, apenas para efeito de cálculos, mas na imagem luminosa o menor ponto que se consiga produzir no objeto será algo como uma nuvenzinha projetada no filme ou sensor.

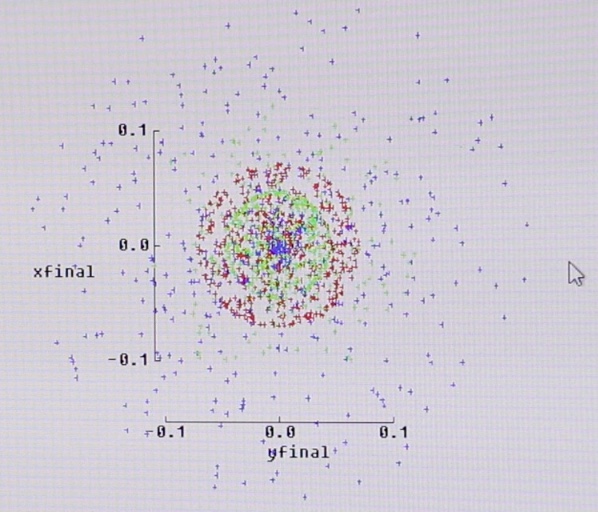
A foto acima é uma captura de tela de um traçador óptico da firma Dioptro, óptica de precisão, de São Paulo. Os raios de curvatura, espaçamentos e índices de refração e dispersão dos elementos de uma lente do tipo Petzval foram colocadas neste software de simulação. Com estes dados da lente o traçador simulou, em poucos segundos, 4000 raios vindos do infinito, isto é, de um ponto hipotético tão distante que seus raios luminosos chegam na lente perfeitamente paralelos. No caso, paralelos também ao eixo da lente, e são por esse motivo focalizados sobre o plano e no centro da imagem. Foram traçadas 3 cores. O verde, por ser o centro do espectro luminoso, o azul e o vermelho por corresponderem aos extremos de menores e maiores comprimentos de onda respectivamente. O que vemos nessa imagem é um “ponto” no objeto quando sua imagem é projetada sobre o plano do filme para uma lente real. O verde está mais concentrado mas o vermelho e o azul já se dispersam por nuvens maiores. As escalas x e y estão em milímetros e podemos dizer, de modo um pouco arbitrário, que este “ponto” tem um diâmetro por volta de 0,15 a 0,20 mm. Mas atenção, este é um ponto no centro do campo. Na prática, é preciso se investigar também o que acontece na periferia, isto é, quando os raios paralelos chegam na lente obliquamente e se dirigem para a borda da imagem. Certamente será algo bem pior que isso e os pontos podem assumir formas elípticas, de setores de um círculo e ainda formas mais complexas.

Essa realidade da “dimensão do ponto” é o que pode ser entendido como “círculo de confusão”. O círculo de confusão é normalmente calculado ou simulado algebricamente em computadores e corresponde ao tamanho real da imagem a partir de um ponto teórico no objeto, como no caso acima. Há um pouco de psicologia da percepção nessas avaliações. Qual é o “tamanho” dessas nuvenzinhas é algo que precisa de certa subjetividade para ser estimado pois ela não tem, obviamente, contornos nítidos como vemos também na figura acima. Isso se resolve quando são estabelecidas convenções que determinam o máximo círculo de confusão que irá gerar uma imagem considerada humanamente nítida e na qual pontos e linhas muito próximas possam ser vistos como distintos. Uma dessas convenções, muito usada em fotografia, diz que o círculo de confusão deve ter no máximo o diâmetro/diagonal da imagem dividido por 1500. Tal regra, baseada em estudos de percepção com pessoas com visão considerada saudável, resulta em uma tabela como esta abaixo para os vários formatos em fotografia (fonte Wikipedia).

Círculo de confusão baseado na regra d/1500

Nome do formato	dimensões	CC
Formatos pequeno
1″ sensor (Nikon 1, Sony RX10, Sony RX100)	8.8 mm × 13.2 mm	0.011 mm
Four Thirds System	13.5 mm × 18 mm	0.015 mm
APS-C	15.0 mm × 22.5 mm	0.018 mm
APS-C Canon	14.8 mm × 22.2 mm	0.018 mm
APS-C Nikon/Pentax/Sony	15.7 mm × 23.6 mm	0.019 mm
APS-H Canon	19.0 mm × 28.7 mm	0.023 mm
35 mm	24 mm × 36 mm	0.029 mm
Médio Formato
645 (6×4.5)	56 mm × 42 mm	0.047 mm
6×6	56 mm × 56 mm	0.053 mm
6×7	56 mm × 69 mm	0.059 mm
6×9	56 mm × 84 mm	0.067 mm
6×12	56 mm × 112 mm	0.083 mm
6×17	56 mm × 168 mm	0.12 mm
Grande Formato
4×5	102 mm × 127 mm	0.11 mm
5×7	127 mm × 178 mm	0.15 mm
8×10	203 mm × 254 mm	0.22 mm

Quando o designer vai então projetar uma lente com um certo ângulo de visão, distância focal, abertura e um “orçamento” em mente, muito importante também considerar os custos posteriores para produção de sua ideia, ele precisará decidir qual será o círculo de confusão que ele irá admitir como viável no centro e periferia da imagem. Normalmente utilizará algo como a tabela acima pois é o padrão da indústria. Mas se ele, por qualquer motivo, escolher um círculo de confusão (CC) muito grande, ele terá maior liberdade para os outros parâmetros da lente, mas terá uma imagem ruim, com pouca nitidez, pois os pontos do objeto irão grosseiramente se embaralhar na imagem. Se ele escolher um valor máximo para o CC bem pequeno, menor que o padrão, pensando em fazer a lente mais nítida do mercado, ele terá que aumentar o orçamento, terá que colocar mais elementos, poderá fechar mais a lente tornando-a mais escura, ou terá que ter uma inspiração divina e criar um novo marco na história das ópticas fotográficas.

Essas convenções e decisões sobre qual deve ser o grau de resolução de uma lente, sobre qual deve ser o seu círculo de confusão, se baseiam em duas hipóteses que são no mínimo razoáveis:

1. Se o fotógrafo vai utilizar uma lente que por sua distância focal e ângulo de visão consegue cobrir um negativo de 8×10″, por que ele iria usar esta lente em uma câmera com negativo ou sensor pequeno, digamos 24×36 mm ou ainda menor? Supõe-se então que a pessoa irá usar a lente para tirar o máximo dela e não uma pequena fração de sua imagem.
2. A segunda hipótese é que se ele vai fazer um negativo 8×10″ ele provavelmente irá precisar de uma ampliação menor dessa imagem pois o negativo já é grande por si só. Um tamanho de álbum de recordações, de exposição, de decoração, de imprensa, de uma tela digital, enfim, o modo de circulação de imagens sub-entende um tamanho que seja confortável e que permita ao observador discernir uma quantidade de detalhes compatível com sua própria capacidade de perceber estes detalhes, nem muito além e nem muito aquém. Este tamanho está novamente mais ligado ao ângulo de visão do que ao formato. Nenhum painel de rua, nenhum outdoor, é feito para ser observado na distância de um braço. Nenhum retrato de parede é feito para ser visto ao microscópio.

Pensando nisso, os designers de lentes admitem um círculo de confusão maior quando a lente se destinar a um formato maior. Essa é uma das moedas de troca por um ângulo de visão mais imponente quando o assunto for grande formato com lentes ditas normais ou grande-angulares

O problema da adaptação

O problema então em se adaptar uma lente de grande formato para ser usada em uma full-frame ou APS-C digital, resolvida a questão física de que ela terá que ser montada a uma distância provavelmente grande do corpo da câmera, coisa que se resolve com tubos ou “pendurando” a câmera digital na traseira de uma grande formato, é que essa lente não irá funcionar tão bem quanto uma lente desenhada para o formato full-frame ou APS-C e outros menores. O círculo de confusão dela será bem maior que o das lentes nativas para o formato pequeno. Isso deve deteriorar a imagem e o fotógrafo tenderá a concluir erroneamente que a óptica não é lá tão boa assim.  Se for uma Tessar, Planar ou uma Apo-Symmar, por exemplo, será certamente uma calúnia. Uma 135, ou 240, ou 300 mm feitas para 4×5″ ou 8×10″ não irão funcionar como “tele-objetivas” para a câmera pequena. Irão, é claro, aproveitar um pedacinho da imagem e esta terá o aspecto que se obtém com lentes longas nas câmeras pequenas, mas a qualidade da imagem não fará justiça ao que a lente de grande formato poder realmente render.

O teste

É claro que uma lente de grande formato fantástica pode eventualmente superar uma objetiva de ângulo estreito fabricada especialmente para o digital. Mas isso seria a excessão. Seria ou porque ela é maravilhosa demais ou porque a digital é ruim demais. O teste que vou descrever abaixo é apenas um exemplo, não prova nada, mas indica e ilustra como que o raciocínio acima vale e acontece.

Zuiko Olympus 300mm f/4.5 montada em uma Sony α7 II

Foram escolhidas para o teste duas lentes 300 mm. A primeira é uma Zuiko da Olympus para o sistema OM. A segunda uma 300 mm Tessar da Zeiss de Jena. O motivo da escolha foi, em primeiro lugar, porque eu tenho essas duas lentes. Mas as coincidências não param aí e creio que no conjunto ficou um teste muito válido. É que as duas lentes são f/4.5, a primeira produção da Zuiko foi em 1974. A Tessar, pelo número de série, foi produzida nessa época também. Isso indica uma certa paridade quanto a tecnologias disponíveis, já que as duas têm procedência de empresas com tradição e renome. Embora o desenho da Tessar seja do início do século XX, ela foi recalculada várias vezes e uma Tessar da década de 70 é uma lente com tecnologia da década de 70. Outro ponto importante para a comparação é que a  Tessar é uma lente cuja característica mais forte é justamente a nitidez, em toda a literatura especializada essa é a característica que sempre se ressalta. Para saber mais sobre ela, siga este link. As duas já tem coating anti-reflexo. A Tessar tem 4 elementos em três grupos, enquanto que a Zuiko tem 6 elementos em 4 grupos. Isso é uma diferença importante a favor da Zuiko, mas o objetivo aqui não é saber quem faz mais com menos e sim o que se pode esperar de duas lentes bem desenhadas por marcas de renome e características semelhantes. A grande diferença entre elas recai mesmo é sobre o ângulo de visão: apenas 8º para a Zuiko e 62º a 72º para a Tessar (conforme a abertura) e consequentemente ao formato a que se destinam uma vez que as duas focam a 300 mm no infinito.

Tessar 300 mm f/4.5 em uma Linhof 13×18 cm

A câmera digital foi uma Sony α7 II, ela tem um sensor full-frame de 6000 x 4000 pixels. Isso é importante pois considerando que o quadro tem 36mm de comprimento temos uma resolução teórica (sem considerar interpolações, grids, etc) de 36/6000 que nos dá 0,006 mm bem abaixo dos círculos de confusão considerados padrão para os formatos aos quais as lentes se destinam (ver tabela acima).

Sony montada no back da Linhof 13×18 cm

Com a Zuiko ela precisou apenas de um anel adaptador (grande vantagem das mirrorless) e para a Tessar ela foi pendurada em uma Linhof 13×18 cm com auxílio do anel da Zuiko e uma peça que imprimi em ABS 3D.

Foram escolhidos 3 alvos/assuntos. Para as duas lentes a abertura escolhida foi f/8. Os arquivos em RAW foram abertos no Photoshop com os ajustes padrão e não foram modificados individualmente. Foram realizadas várias fotos de amostra para entre elas para se escolher aquela com melhor aparência por conta do foco manual.

O primeiro assunto foi um grupo de antenas no alto de prédios muito distantes. As duas lentes/câmeras foram montadas em tripés Gitzo bem robustos.

Fazendo a foto com a Tessar

 

Quadro cheio: Zuiko 300 mm em f/8

Quadro cheio: Tessar 300 mm em f/8

Obviamente o enquadramento é o mesmo já que estamos apenas “jogando fora” a maior parte da imagem da Tessar. Já notamos diferenças a favor da Zuiko mas ainda no território em que um ajuste de curvas e sharpness poderia ajudar bastante. Mas é no detalhe abaixo que vemos o quanto a lente de Grande Formato está perdendo. Na próxima foto temos uma imagem recortada em 300 x 300 pixels. Se você estiver vendo em um monitor de desktop ou lap-top provavelmente estará vendo em 100%, isto é na relação ideal de 1:1, 1 pixel no arquivo correspondendo a 1 pixel na tela.

Fica muito evidente que há uma perda de resolução no caso da Tessar.

O segundo teste foi com um objeto na sombra com o objetivo de termos também uma situação de baixo contraste.

Simplesmente baixei o eixo da câmera e focalizei na placa de estacionamento que se vê nas fotos abaixo. Observando as fotos com o quadro cheio, vemos que sem o contra-luz, que é sempre uma situação difícil para uma lente, parece que a Tessar recuperou mais terreno em relação à Zuiko.

Quadro cheio: Zuiko 300 mm em f/8

Quadro cheio: Tessar 300 mm em f/8

Porém, quando olhamos novamente no detalhe vemos que o corte da Zuiko se sai muito melhor. Há um efeito de flare que cria uma névoa mais pronunciada na Tessar, porém, a questão do círculo de confusão, que nela é certamente maior, é o real responsável pela suavização dos contornos, das passagens das letras impressas para o fundo. Um flare aleatório apenas reduziria os contraste como um todo.

A terceira situação foi dentro de casa a uma distância de 5 metros, mais ou menos.

Coloquei uma caixinha de analgésico junto a esse elefante de louça que tem sido meu modelo em tantas outras fotos. As fotos abaixo não foram feitas logo em seguida e por isso a coloração mudou com o dia pois era luz natural. O enquadramento também não foi rigorosamente o mesmo e por isso há uma diferença de tamanhos nas imagens da caixinha de analgésico. Mas é possível ainda se comparar.

Quadro cheio: Zuiko 300 mm em f/8

Quadro cheio: Tessar 300 mm em f/8

Em distâncias curtas o mesmo efeito se observa. Como as letras são brancas sobre um fundo vermelho o círculo de confusão maior cria um efeito de halo para elas.

Conclusão

Tudo que se pode dizer com certeza é que se for para aproveitar apenas 24 x 36 mm da imagem, a 300 mm f/4.5 Zuiko gera uma nitidez muito superior à Tessar 300 mm f/4.5. Pelo menos este caso confirma a expectativa deduzida teoricamente de que o projeto de uma lente de grande formato, destinada a cobrir um ângulo grande, no caso de ~62º, irá precisar abrir o círculo de confusão muito mais do que o projeto de uma lente que irá cobrir apenas 8º. A consequência é um embaralhamento dos pontos locais e perda de nitidez.

Será que existe alguma lente caríssima, Apo qualquer coisa, que seria capaz de rivalizar com uma objetiva nativa para o formato digital? Eu duvido muito. Podemos concluir daí que a Tessar não é uma boa lente? De forma alguma. Olhando aqui na minha tela enquanto escrevo, eu vejo que essa imagem de 300 x 300 px tem 77 mm na tela do meu computador. Como a Sony α7 II tem 6000 px em 36 mm, fazendo as contas, vemos que estes 77 mm correspondem a 1,8 mm do captador, ou seja, 1,8 mm da imagem da Tessar. Mas a imagem total da Tessar, se jogarmos 300 mm de focal e 62º de ângulo de visão nesta ferramenta, temos um círculo de imagem de 361 mm. Vamos dizer 300 mm de diagonal para um quadro 18 x 24 cm, já que as imagens fotográficas raramente são circulares. Então esses 1,8 cabem 133 vezes nos 24 cm da imagem (240 mm ÷ 1,8 mm). Multiplicados por 77 mm, isso dá 10,2 metros ! Estou olhando para um pedaço de imagem que no total poderia ter 10,2 metros se eu estivesse aproveitando todo o campo da Tessar! Ora, não é nada mal essa Tessar, certo? Imagens de 10 metros não são para se olhar a 30 cm de distância como eu estou fazendo nesse momento.

A conclusão final então é que se for para otimizar a qualidade de uma imagem a melhor estratégia é usar lentes projetadas e fabricadas para o formato em que estamos fotografando. Se for para se divertir, é claro que vale tudo. Mas divertido mesmo será quando tivermos sensores digitais de grande formato a preços acessíveis. Aí sim será a hora e a vez, será a revanche das vintage que irão poder mostrar toda a sua excelência. Aguardemos.