Entenda distância focal, ângulo de visão e círculo de imagem

(image source: wikimedia commmons)

Você certamente já viu um diagrama mais ou menos como esse, mostrando a relação entre distância focal e o ângulo de visão que a lente alcança. É um jeito que se tornou padrão para explicar distância focal. Essa é a forma como os fabricantes de câmeras falam de distância focal e eles tem uma boa razão para isso: precisam apenas que você entenda o que é distância focal no contexto dos produtos que eles vendem, não necessariamente em óptica ou fotografia.

O que você está perdendo se assumir isso como distância focal? Bem, você fica amarrado ao tipo de câmera ao qual esses diagramas se referem e terá que aprender a fazer umas conversões de “distância focal equivalente” e coisas assim, se quiser pensar em outros formatos, lentes e câmeras. Por que então não aprender diretamente o que é de fato distância focal e pensar fotografia, lentes e câmeras, de modo mais livre? A maneira certa de falar sobre isso envolve distância focal juntamente com outro conceito chamado círculo de imagem. Estes dois, em conjunto com a abertura, são os três parâmetros chave que descrevem uma lente fotográfica. Existe ainda o círculo de confusão, mas não vamos falar nele agora. Neste post nós iremos examinar apenas a distância focal e o círculo de imagem.

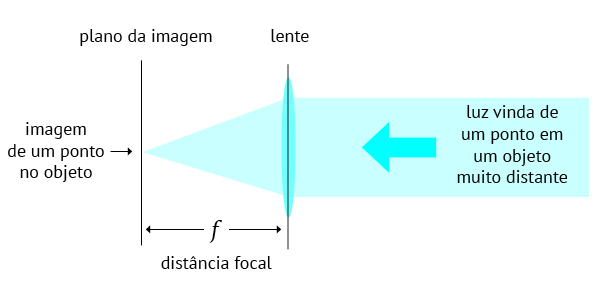
Você também já deve ter visto diagramas como esse acima. Esse é o que corretamente ilustra o que distância focal é realmente em uma lente fotográfica. Pode ser enunciado da seguinte forma:

Distância focal, em uma lente fotográfica, é a distância axial entre o centro óptico da lente e a imagem quando o objeto focado está longe o bastante para ser considerado a uma distância infinita.

Confuso? Bem, vamos nos aprofundar mais um pouco e ficará intuitivo. Vamos considerar uma pequena estatueta como nosso objeto e estudar como que imagem de uma lente fotográfica se forma para um ponto qualquer entre as suas sobrancelhas. Vamos considerar um único ponto apenas para simplificar e tornar os diagramas legíveis, mas o princípio é o mesmo para todos os pontos em um objeto ou em uma cena. Como você sabe, uma lente fotográfica é um aparato óptico com um certo poder de fazer convergir a luz. Se isso não é familiar para você, leia antes O que faz uma lente fotográfica? A animação a seguir mostra como esse poder de convergência trabalha a luz que, vinda de um ponto qualquer, atinja a superfície da lente.

Vamos analisar o que a animação mostra:

1. No início, o ponto observado está muito próximo da lente, então a luz que diverge a partir dele o faz tão abruptamente em direção à lente que mesmo com esta aplicando o seu poder de convergência ela não é capaz de fazer com que estes raios de luz convirjam sobre a imagem, no filme ou sensor digital. Podemos notar que ela converge mas não o bastante. Ela iria formar uma imagem pontual em algum lugar além da traseira da câmera.
2. Quando o objeto começa a se afastar da lente, sua luz diverge mais suavemente em sua direção. Como consequência a lente, com seu poder de convergência fixo, começa a convergir esses raios em um ponto mais e mais próximo a ela.
3. Quando o ponto está tão longe, fora do quadro da animação, e nem podemos mais perceber se estão divergindo ou paralelos, o poder de convergência da lente é justo o que é preciso para capturar essa luz e fazer com que ela se concentre em um único ponto na imagem, precisamente sobre o filme o sensor digital.
4. Essa é exatamente a situação descrita na definição de distância focal. Nós podemos então dizer que a distância entre a lente e a imagem é a distância focal, normalmente representada pela letra f.
5. Quando a estatueta volta, a mesma situação inicial deveria se apresentar. O poder de convergência sendo o mesmo, ele irá enviar a imagem para um ponto além do corpo da câmera. Mas desta vez, a lente avançou e compensou a proximidade do objeto para formar a imagem bem onde ela deve ser formada: sobre o filme ou sensor digital. Esse é o método básico pelo qual lentes são capazes de focar objetos que não estão tão distantes a ponto de os considerarmos no infinito. Ou a lente avança em direção ao objeto, ou a traseira da câmera recua, ou as duas coisas.

Distância focal e ângulo de visão

Podemos notar agora que distância focal é um número, um parâmetro muito importante para uma lente e que em primeiro lugar não tem relação nenhuma com o ângulo que a lente abraça. O que uma lente intrinsecamente tem, de acordo com sua construção, é uma distância focal e um ângulo de visão que são independentes um do outro. O ângulo de visão é determinado pelo tipo de construção e desenho da lente. Quando ele passa de 60º, nós a chamamos de lente  angular, ou grande angular se passar muito. No início da história da fotografia esse era um assunto de quem queria desenvolver lentes para fotografia de paisagens. Com menos de 30º nós podemos dizer que se trata de uma lente com um ângulo estreito, fechado. Historicamente essas seriam as lentes dedicadas a retratos.

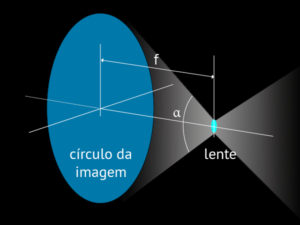
Para uma dada distância focal o ângulo de visão irá determinar o que se chama de círculo de imagem da lente. É fácil perceber que uma vez que f e α estejam determinados, o círculo de imagem também estará fixado. Lentes angulares famosas como a Pantoskop, de Emil Busch (1820-1888), cobria 80º e o mesmo desenho foi fabricado em sete tamanhos diferentes com distâncias focais indo de 52 até 540 mm (fonte Kingslake)

Acima, nós temos uma típica imagem projetada por uma lente fotográfica. É um círculo e o quadro de contorno branco representa o que uma câmera pode usar se uma imagem na proporção 3:2 for desejada. Os cantos do quadro quase tocam a borda do círculo. O fabricante de câmeras podem usar uma porção menor da imagem fazendo o filme ou sensor digital menores que o círculo de imagem. Esse será o caso se ele estiver desenhando uma câmera que permita movimentos da lente como deslocamentos e inclinações – se não for para isso, seria apenas  um desperdício. Esse é o caso da maioria das câmeras de  vidro despolido e também de algumas modernas (e caras) lentes para máquinas digitais que permitem o que se convencionou no Brasil se nomear no inglês: shifts & tilts (deslocamentos e inclinações).[/mks_one_half][/mks_col]

Fabricantes de câmeras precisam usar lentes que projetem imagens com um círculo de imagem que seja maior que o tamanho da foto (filme ou sensor), se isso não acontecer, a imagem irá perder brilho nos cantos e ficará com um efeito de vinheta. Lentes angulares são mais complicadas e mais caras pois fica mais difícil nelas se controlar as aberrações a não ser que se sacrifique muito a abertura. A Pantoskop, mencionada mais acima, tinha a limitante abertura de apenas f/25. Lentes com ângulo de visão mais estreito são mais simples e demandam menos em termos de vidros e desenho. São também mais fáceis de produzir com aberturas mais generosas. Os vidros têm raios de curvatura maiores nas lentes longas ao passo que nas curtas as curvas são bem mais acentuadas. (foto acima, paisagem com árvores, fonte:  Wikimedia Commons, autor: Balkhovitin).

Duas lentes 300 mm muito diferentes entre si

A  Zeiss Protar – Ross e a teleobjetiva Olympus Zuiko acima, são ambas 300 mm. A primeira cobre um ângulo de 70º e a segunda 8º. A primeira é uma grande angular de 300 mm e a segunda é uma teleobjetiva de 300 mm. O que isso significa? Significa que o desenho da Protar permite que ela seja colocada em uma câmera usando filme 180 x 240 mm (normalmente se usa 18 x 24 cm, para essa medida) e ainda sobra espaço para deslocamentos e inclinações pois o diâmetro do círculo de imagem mede 42 cm quando focada no infinito. Isso é muito mais do que a diagonal do retângulo de 18 x 24 cm (que mede 30 cm). A teleobjetiva Olympus Zuiko, é também uma 300 mm, mas o seu círculo de imagem é apenas o necessário para cobrir uma imagem de 24 x 36 mm. O diâmetro de seu círculo de imagem com certeza deve passar pouco de 43,27 mm, pois esta é a diagonal de um retângulo de 24 x 36 mm. Qualquer coisa acima disso seria desperdício de recursos para o tipo de câmera à qual a lente se destina. Normalmente há uma pequena folga para se evitar que os cantos comecem a escurecer, mas é apenas o mínimo necessário para que isto não aconteça.

Uma observação sobre lentes chamadas “tele-objetivas”. O que chamamos teleobjetivas é um tipo especial de lente que é fisicamente mais curta que a própria distância focal. Isto significa que uma lente, por exemplo, teleobjetiva de 300 mm não precisa de 300 mm entre a imagem e seu corpo. Seu centro óptico sim, este precisa de 300 mm até a imagem, mas ele fica na verdade à frente da lente e fora dela.

Ferramentas para você

Agora que você já entendeu o que é distância focal, ângulo de visão, círculo e formato da imagem, talvez queira fazer algumas comparações e descobrir esses parâmetros nas suas lentes e câmeras. É fácil fazer essas contas. A matemática envolve o teorema de Pitágoras e alguma trigonometria bem básica. Mas, para ficar ainda mais fácil, aqui vão algumas ferramentas prontas para usar e calcular estes parâmetros:

Calcular o círculo de imagem de um formato. Você sabe qual é o formato da sua câmera, do quadro do filme ou sensor digital, e quer saber qual é o círculo de imagem mínimo para cobrir este formato, ou seja, qual é o círculo de imagem da sua lente. Siga este link: Círculo de imagem mínimo para um dado formato.

Calcular o ângulo de visão. Você já sabe a focal de sua lente e o formato do filme ou sensor e gostaria de saber qual é o ângulo de visão da sua lente. Se ela for zoom, pode calcular o mínimo e o máximo. Siga este link: Ângulo de visão para uma lente fotográfica baseado no círculo de imagem e distância focal.

Calcular o círculo de imagem de uma lente. Você sabe a distância focal de sua lente, pesquisou no manual ou ficha técnica qual é o seu ângulo de visão e gostaria de saber qual é o seu círculo de imagem. Siga este link: Círculo de imagem a partir do ângulo de visão e distância focal.

Calcular a distância focal de uma lente. Na maioria das lentes modernas isso vem escrito no anel frontal. Mas se você estiver com alguma gema preciosa do século XIX (quando habitualemte não se gravava a focal no corpo da lente) ou quer usar uma lupa ou lente qualquer que encontrou como lente fotográfica, siga este link e veja com calcular experimentalmente a distância focal de sua lente: Como descobrir a distância focal de uma lente.

Avançado

Agora uns cálculos úteis para quem faz grande formato

Linha do Horizonte e elevação da lente. Quando você faz uma foto com o eixo da lente na horizontal, no nível, a linha do horizonte, visível ou não, divide o quadro exatamente ao meio. Muitas vezes você quer subir a lente (front raise) para manter as linhas verticais da cena verticais na imagem também, pois se inclinar a câmera estas verticais irão convergir em algum ponto no céu. Uma informação interessante quando se escolhe uma lente pode ser até onde é possível se baixar a linha do horizonte fazendo-se um front raise sem vinhetar a imagem. Para ter esse cálculo siga este link: Elevação da lente e a Linha do horizonte.

Enquadramento. Você conhece a distância focal, abertura que quer usar, formato do filme ou sensor, altura e/ou largura do que quer fotografar e deseja saber que distância terá que tomar do objeto, de onde até onde terá foco, quanto terá que avançar a lente (tamanho do fole) e quanto terá que compensar a exposição se esticar muito o fole. Siga este link: Simulador de enquadramento, profundidade de campo e distâncias em fotografia.

A lente Normal

Com frequência ouvimos falar em lente normal.  Lente normal é aquela que não é nem angular e nem longa. Ela corresponde mais ou menos à visão humana se considerarmos nosso campo de visão mais central. Em números, isso corresponde mais ou menos a um ângulo de visão de 45%. Traduzido para formato e focal seria a lente de 50 mm para o filme 35 mm em full-frame (24×36 mm). Se você usar as ferramentas listadas acima verá que esse formato com uma lente de 50 mm dá na verdade um ângulo de 47º, mas essas coisas são aproximadas. O resultado é que quando olhamos pelo visor de uma câmera com uma lente normal não temos a impressão de que os objetos ficaram significativamente maiores (objetivas longas) e nem menores (objetivas curtas ou angulares). A câmera, com a lente normal, dá uma imagem que corresponde bem ao que vemos a olho nú.

Conciliando as representações de distância focal

Nesse ponto já podemos entender que os dois diagramas mostrados na abertura deste post não estão de fato em conflito. Nós podemos concilia-los se considerarmos este novo diagrama combinado:

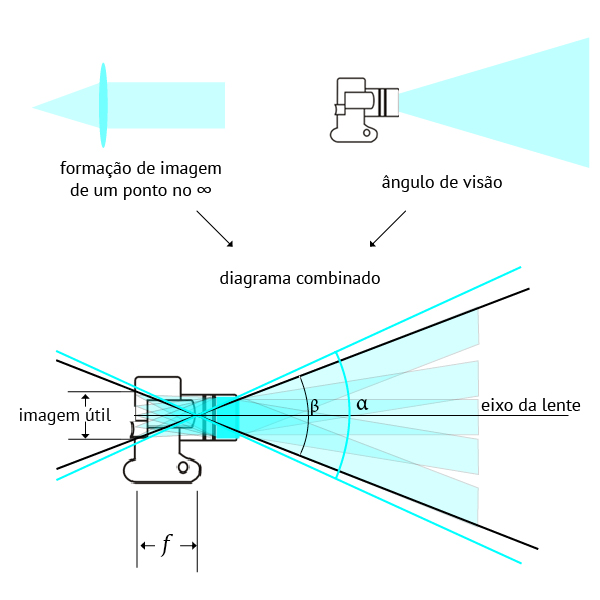
Este não é um desenho técnico, não foram utilizadas fórmulas – é mais uma ilustração. O que ela mostra é que o diagrama com o ângulo de visão da câmera é como que a superposição de vários (infinitos) diagramas com a formação de imagem para pontos em uma cena distante.

Notar que o  ângulo de visão da câmera β é um pouco menor que o ângulo de visão da lente α. Isso é para garantir que o filme ou sensor digital caibam dentro do círculo de imagem da lente e não haverá cortes nos cantos. É um pouco menor em câmeras que não permitem movimentos e bem menor em câmeras que permitem movimentos da lente ou do filme/sensor. Se você compreendeu esta frase, então você entendeu o que é distância focal independente de marcas ou formatos.

O mesmo raciocínio aplica-se para se entender as diferenças entre sensores digitais APS-C e full-frame. Enquanto que o formato do primeiro é 16.7 x 25.1 mm, o segundo mede 24 x 36 mm. As lentes desenhadas para full-frame tem círculo de imagem maior do que é necessário para encher um sensor APS-C, enquanto que a recíproca não é verdadeira. Uma lente para full-frame irá funcionar em um sensor APS-C, mas o inverso, não é verdade. Se alguém der um jeito de fixar uma lente para APS-C em uma câmera full-frame, haverá um efeito de vinheta produzindo cantos escuros na imagem.

Por que lentes não são feitas para que sejam sempre cheias de cobertura e grandes círculos de imagem? Dada uma certa distância focal e esperada qualidade de imagem, os custos de produção crescem como círculo de imagem. Como foi dito antes, as angulares são as mais complicadas para se fazer. Por essa razão os fabricantes não desenham lentes que cubram mais do que é necessário de acordo com o formato do sensor digital que a câmera usa. Além de ser inútil e mais caro, isso ainda demandaria implementar barreiras e armadilhas para evitar que a luz não utilizada termine, por reflexões internas, atingindo e piorando a qualidade da imagem.

Algumas pessoas estão adaptando lentes feitas para grande formato em câmeras digitais com seus sensores pequenos. À primeira vista isso parece bem viável, mas na verdade implica em uma perda considerável de qualidade. É fato que “sobra imagem” mas a definição de uma lente feita para uma câmera de grande formato não é a mesma, é usualmente bem menor que o que se exige para câmeras pequenas. Veja um experimento mostrando essa diferença no artigo: Lentes de grande formato em câmeras pequenas.

Com a introdução de formatos médios em sensores digitais, como o que equipa a Hasselblad H5D-200c que possúi 50MP em um sensor CMOS de 43.8 x 32.9mm, e também chassis digitais para câmeras de filme, a natureza verdadeira de distância focal e círculo de imagem precisam ser entendidas se não quisermos ficar decorando um monte regrinhas de conversão. Os fabricantes de câmeras não gostam nem um pouco de promiscuidade entre corpos, lentes e marcas. A montagem em baioneta é a maneira pela qual eles tentam evitar isso. Mas ao longo da história da fotografia, exatamente a possibilidade de misturar formatos de filmes com diversas lentes, tem sido parte da diversão, da criatividade e dos mistérios do meio. Então, como a fotografia digital ainda está na sua infância, vamos aguardar o tempo em que serão produzidos sensores com tamanhos e preços que permitam fotógrafos utilizar apenas uma chapa com um buraco no meio e nele colocar a lente que bem tiverem vontade de experimentar.