Finding the focal length of a lens

This is a calculator that will help you in finding the focal length of a photographic lens. The method is about focusing on one or more objects at different distances. Each time, you write down 3 measurements. Only one measurement could do. But the idea is that “averaging” several instances it will yield a more precise figure.

1. Object size
2. Image size
3. How much did you advance the lens from infinity position in order to get focus.

The application may be especially useful for old lenses, those of which do not present the focal length written on them. This happens for most of the lenses manufactured in the nineteenth century. For decades, even in technical specifications in catalogues, the habit was to inform the format covered and whether it was for portraits or landscapes, but not the focal length. Like, for example, the Darlot on the left. The calculator also helps in do-it-yourself projects when magnifying glasses, projection lenses or any other type of lens for which we do not know the focal length is used. Follow the step-by-step described below.

1Mark the point at which your lens is focused at infinity. This can be done by focusing a very distant object. But be aware, the distance must be really far away, buildings, trees or light poles may be good targets for this. Choose the farthest that still produce a sharp image to be precisely focused.

2Next you will make various measurements focusing on nearby objects. For each position, it will be necessary to measure the distance the lens has been tripped. In the photo below a small piece of wood was fixed with a clamp so as to create a gap that has exactly the measure of how far the lens has advanced to focus. When at infinity, it touches the drop bed. When we turn the knob to focus, it moves away and then we have a gap, convenient to measure, and that represents the correspondent displacement. In this case, 27.12 mm with a digital caliper.

3You will also need to measure the size of the focused object and its corresponding image. Colored adhesive tapes attached to a window glass or wall can be great for this purpose. You can create two targets: one should be easy to focus on (making a star is a good solution), the other would then be the one to measure – a horizontal ribbon is the trivial case. It is important to have both in the same plane perpendicular to the axis of the lens and their images more or less in the center of the ground glass.

In the photo above the focus was made on the star, with the help of a loupe, and the measurement of the horizontal tape was performed with a digital caliper. In cases of close approximation, when the image of the horizontal tape can be larger than the ground glass, a smaller tape can be placed. When the camera is too far apart and inversely the image becomes very small, one can use a larger tape or measure the window itself.

4The calculator holds up to 12 measures. It’s more than enough. The distance from the camera should be varied from an almost close-up situation up to the limit that provides an image still measurable. Once this is done, just fill up the form at the top of this article with every set of values: object size, image size, lens shift. Then click “calculate”. You can edit the data if you note something strange, or in case you want to insert more sets or delete some that clearly presents an error. Just correct, insert or delete and click calculate again.

5Analysis: The interesting thing about this method is that it provides a visual impression of how consistent the data is. After clicking on calculate you should get something like this:

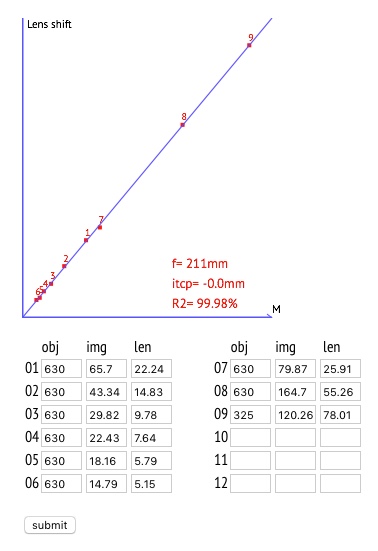
The statistically calculated focal length is shown on the graph itself. 211 mm in this case. If the dots are aligned, this is a good indicator that your measurements have been well made and the focal length obtained is reliable unless for a very small error. In this example above, it was a Tessar 210 mm which was used only to evaluate the method. In general the lenses were made with round numbers. If you find 178 or 179, it may, or could be, marked as 180 mm, the difference is a fluctuation either on the lens making or in your measurements. A survey of the lens itself and its manufacturer can complete what the measurement already indicated. But there are exceptions, such as a Wollensak Raptar, which has a focal length of 241 mm.

Theory

The basis of this calculation is the fact that the displacement necessary to focus on an object closer than infinity is proportional to the magnification provided for the object. In the graph representing this relation, the angular coefficient (slope) of the line is precisely the focal length.

The operation is then simply about doing a linear regression of the given data considering that:

Magnification = Image size / Object size

and

Lens displacement = Focal Length x Magnification

The regression method finds the line equation that best fits the sample of given values. Two parameters a and b, in the function below, are calculated by the least squares method:

Y = ax + b

One might ask why not an equation of the type y = ax, since we know in advance that the line must pass through the origin. The reason is that if there is an error, however small, in determining the position at infinity, this error will introduce a theoretically equal deviation in all measurements. It will pull them up or down. In these cases the ideal line adjusted to the points will not pass through the origin. However, its slope, and that is what we are after, will be the same and equal to focal length.

This highlights the fact that the position at infinity is not so important and only the measured values ​​in relation to any point already provide the focal distance. The term itcp, shown in the graph, is precisely the value at which the line intercepts the y-axis. If it is too large, positive or negative, it is a good indication that it would be better to check the point marked as being focus at infinity. If it is positive it should be more retracted and if it is negative more advanced in relation to the film.

R2 is a numerical parameter that indicates how well the data fit the line. 100% means a perfect fit. It is useful in the event that you redo a new set of measurements for the same lens and want to have a numeric means to evaluate which one is best aligned.